Tentukan himpunan penyelesaian dari sistem persamaan linear berikut dengan menggunakan metode eliminasi:
Penyelesaian:
Soal 2Gunakan metode substitusi untuk menentukan himpunan penyelesaian SPLDV berikut!
2x + y = 6
x – 2y = 8
Penyelesaian:
Jadi, himpunan penyelesaian dari SPLDV tersebut adalah {14/3, -5/3}.
Soal 3Gunakan metode grafik untuk mencari penyelesaian SPLDV berikut.
Jawab:
Untuk memudahkan menggambar grafik dari x – y = 1 dan 3x – y = 6, buatlah tabel nilai x dan y yang memenuhi kedua persamaan tersebut.
x – y = 1
x
|
0
|
1
|
y
|
-1
|
0
|
x, y
|
(0, -1)
|
(1, 0)
|
3x – y = 6
x
|
0
|
2
|
y
|
-6
|
0
|
x, y
|
(0, -6)
|
(2, 0)
|
Grafik:
Gambar di atas adalah grafik sistem persamaan dari x – y = 1 dan 3x – y = 6. Dari gambar tampak bahwa koordinat titik potong kedua garis adalah
Jadi, himpunan penyelesaian dari sistem persamaan dari x – y = 1 dan 3x – y= 6 adalah
Soal 4Zainal dan zainul jalan jalan ke pasar minggu. Mereka berhenti di stan buah untuk membeli buah. Anak kembar ini kompak memilih buah jeruk dan buah mangga. Zainal membeli 2 buah mangga dan 3 buah jeruk membayar Rp 6.000,- kemudian zainul mengambil 4 buah jeruk dan 5 buah mangga membayar Rp 11.500,-. Tentukanlah berapa harga satu buah mangga dan satu buah jeruk yang dibeli zainal dan zainul dengan menggunakan metode eliminasi!
Penyelesaian:
Diketahui : 2 buah mangga dan 3 buah jeruk Rp 6.000,-
4 buah jeruk dan 5 buah mangga Rp 11.500,-
Ditanya: Berapa harga 1 mangga dan harga 1 jeruk?
Jawab :
Misalkan : Harga 1 mangga = x
Harga 1 jeruk = y
a. Model matematika:
2x + 3y = 6.000
5x + 4y = 11.500
b. Eliminasi variabel x, maka :
Jadi, harga satu mangga adalah Rp 1.500,00 dan harga satu jeruk adalah Rp 1.000,00.
Soal 5
Dengan metode gabungan, tentukan himpunan penyelesaian dari sistem persamaan 2x – 5y = 2 dan x + 5y = 6, jika x, y ∈ R.
Jawab:
Langkah pertama yaitu dengan metode eliminasi, diperoleh
Selanjutnya substitusikan nilai y ke persamaan x + 5y = 6, sehingga diperoleh
Jadi, himpunan penyelesaian dari persamaan 2x – 5y = 2 dan x + 5y = 6 adalah
Soal 6
Harga 1 kg beras dan 4 kg minyak goreng Rp14.000,00. Sedangkan harga 2 kg beras dan 1 kg minyak goreng Rp10.500,00. Tentukan:
a. model matematika dari soal tersebut,
b. harga sebuah beras dan minyak goreng,
c. harga 2 kg beras dan 6 minyak goreng.
Penyelesaian:
· menentukan nilai x dan y.
Dari uraian tersebut diperoleh:
x = harga 1 kg beras = Rp4.000,00
y = harga 1 kg minyak goreng = Rp2.500,00.
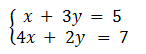














Komentar
Posting Komentar